Bellův test jako „dvojštěrbina pro dva“

Newton věřil, že světlo jsou částice – malé kuličky létající prostorem. Pak přišel Youngův dvojštěrbinový experiment (1801) a ukázal interferenční proužky – důkaz, že světlo je vlna. Celé 19. století se fyzici radovali: světlo jsou vlny šířící se éterem, vesmír je mechanický a předvídatelný.

Jenže pak přišel rok 1905. Einstein zrušil éter (speciální relativita) a paradoxně vrátil světlu částicovou povahu (fotoelektrický jev). Kvantová mechanika šla ještě dál – světlo je vlna i částice zároveň, podle toho, jak se ptáte. To vedlo k rozkolu: Einstein a spol. věřili, že za kvantovou neurčitostí se skrývá hlubší, deterministická realita ("Bůh nehraje v kostky"). Bohr a kodaňská škola byli radikálnější – tvrdili, že realita před měřením vlastně neexistuje, existují jen pravděpodobnosti. Není to podle ní jen naše neznalost; samotná příroda "neví", dokud se nezeptáte.

V roce 1964 přišel John Bell s geniálně jednoduchým testem: pokud má Einstein pravdu a částice mají předem dané vlastnosti ("skryté proměnné"), musí jejich korelace splňovat určité matematické nerovnosti. Pokud má pravdu kvantová mechanika, tyto nerovnosti můžou být porušeny.

Tento test vznikl z frustrace fyzika Johna Stewarta Bella v 60. letech, který nebyl spokojen s tím, jak kvantová mechanika popírala "zdravý rozum" – konkrétně myšlenku, že částice mají určité vlastnosti nezávisle na měření (lokální realismus). V roce 1964 formuloval matematickou nerovnost, která umožňovala experimentálně rozlišit mezi kvantovou mechanikou a teoriemi se skrytými proměnnými, které by zachovávaly lokální realismus, který razil mimo jiné Einstein. Když v 70. a 80. letech mnozí fyzici jako třeba Alain Aspect skutečně provedli tyto experimenty, výsledky jednoznačně porušily Bellovy nerovnosti, čímž potvrdily předpoklady kvantové mechaniky.

Věda je silná poctivou metodou. Takže Bell sice formuloval tezi, která nakonec vedla k pravému opaku, než ve který doufal, ale tak to někdy chodí. On sám k tomu pak říkal: "Pro mě je tak rozumné předpokládat, že fotony v těchto experimentech si s sebou nesou programy, které byly předem zkorelované a říkají jim, jak se mají chovat. Je to tak racionální, že si myslím, že když to Einstein viděl a ostatní to odmítali vidět, byl to on, kdo byl racionální. Ti druzí, ačkoliv jim historie dala za pravdu, strkali hlavu do písku... Takže pro mě je škoda, že Einsteinova myšlenka nefunguje. Ta rozumná věc prostě nefunguje."

O co přesně jde? Pokud platí:

1. měření na jedné částici nemůže okamžitě ovlivnit výsledek měření na vzdálené částici

2. fyzikální vlastnosti existují všechny samy o sobě a nezávisle na měření

3. experimenty lze nastavit nezávisle na skrytých proměnných

pak musí korelace mezi měřeními na propletených částicích splňovat Bellovy nerovnosti.

Jaký tedy je výsledek experimentů? Nerovnosti jsou porušeny! Einstein se tedy mýlil – ale jinak, než všichni čekali. Příroda nefunguje ani klasicky (vše předem určeno), ani čistě náhodně, a přitom vytváří korelace silnější, než by jakýkoli klasický systém dokázal.

Okamžitě se samozřejmě objevily divoké interpretace – telepatie, okamžitá komunikace, vědomí ovlivňující realitu. Skutečnost je prozaičtější, ale hlubší: částice na opačných koncích galaxie mohou být "na stejné vlně", aniž by si vyměňovaly jakékoli signály. Místní měření dávají náhodné výsledky, ale když je porovnáte, najdete v nich skrytý vzorec souznění, který klasická fyzika nedokázala vysvětlit.

Poznámka autora: Sám jsem těmto divokým interpretacím podlehl a trochu je i zde šířil. Bylo to lákavé: vědomí jako prvotní a fyzikální realita jako odvozená dávají filozoficky smysl. Berkeleyho "esse is percipi" ale neobstojí jako fyzikální konstrukce. Krásné stvoření fyzikálního vesmíru funguje samo o sobě a nepotřebuje k tomu vědomého pozorovatele. Přesto celým srdcem věřím, že vesmír byl stvořený proto, abychom se z něj mohli radovat a učili se ho poznávat a milovat. Ale nic z toho se nezdá být fyzikálně potřebný pohled a z kvantové mechaniky samotné vědomí odvodit dle mého ve skutečnosti opravdu nelze.

Jsem, tedy myslím - Blogosvět.cz

www.blogosvet.cz

Vynálezce mikroprocesoru, který zjistil, že realita je stvořena z vědomí. Zní to jako sci-fi? A přece je to příběh Federica Faggina, muže, který změnil svět dvakrát. První revoluci způsobil, když dal světu první mikroprocesor a dotykové displeje. Druhou, když po mystickém zážitku u jezera Tahoe v prosinci 1990 zcela přehodnotil svůj pohled na realitu. Během této neobyčejné zkušenosti zakusil, že on sám není oddělen od světa, ale obojí je utvářeno stejnou vědomou energií. Faggin, který vyrostl v katolické rodině italského učence překládajícího díla antických filozofů, propojil své technické mistrovství a duchovní vhled do teorie vědomí vesmíru. Společně s fyzikem D'Arianem dnes tvrdí něco, co obrací moderní materialistickou vědu naruby: vědomí není produktem hmoty, ale naopak hmota je projevem vědomí.

Jádro principu

Klasický pohled: předem dané odpovědi a sčítání pravděpodobností. Kvantový pohled: jedna společná „vlna" pro celou dvojici a sčítání amplitud. Bellův test zjišťuje, jak realitu dvou vzdálených výsledků vystihne „kartičkový plán" (klasika), nebo skládání jedné společné vlny (kvantum).

Pozn.: Ve vzorcích používám radiány; ve větách uvádím úhly ve stupních kvůli čitelnosti.

Klasické rukavice vs. kvantové dvojice

Klasické rukavice

Když rozdělíš pár rukavic do dvou krabic a pošleš je na opačné konce světa, v jedné je levá a v druhé pravá. Bylo to rozhodnuto už při balení – ty jen dodatečně zjistíš, která je kde.

Kvantové dvojice

U zvláštních kvantových dvojic, které jsou doslova na stejné vlně, a ne na dvou různých vlnách, nejde vše vysvětlit tak, že by každá polovina měla dopředu dopsaný plán odpovědí pro všechny možné volby měření. Když změříš jednu, u tebe se ukáže konkrétní výsledek; na druhé straně se místní poměry nezmění a nejde tím posílat zprávy. Teprve když dáte záznamy dohromady, vyjde vzorec shod/neshod silnější, než by dovolil jakýkoli předem daný plán.

Různé interpretace

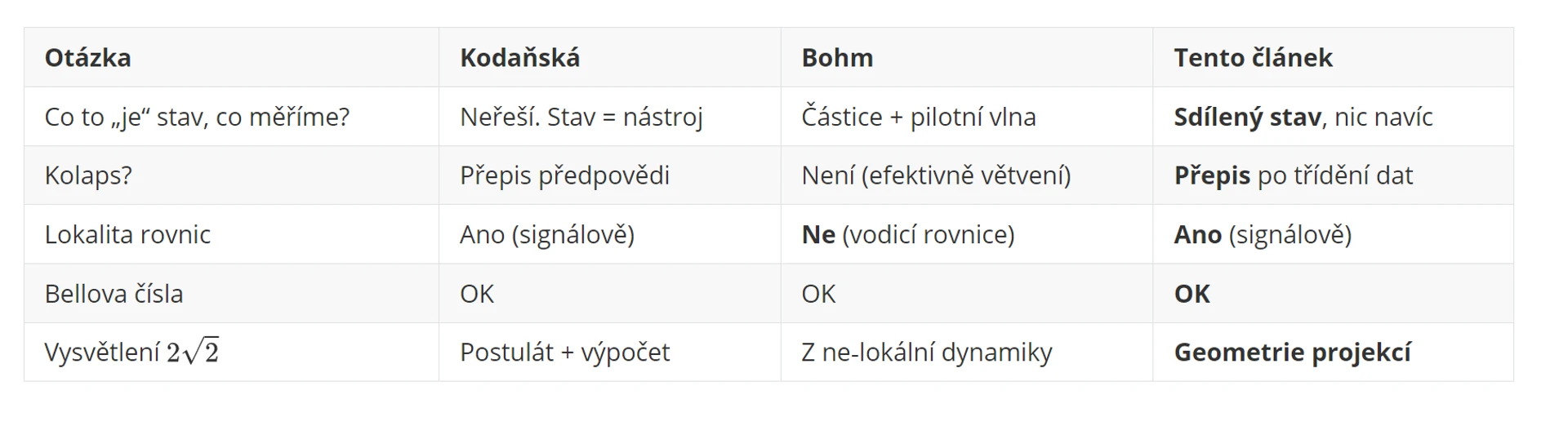
Než přejdeme k matematickému popisu, který možná mohé čtenáře odradí, zkusme si nejprve nějak představit, o co se v případě kvantové provázanosti částic jedná. Momentálně se převažující interpretace dívá na tuto oblast tak, že dochází ke "kolapsu vlnové funkce". To ale není nějaká fyzikální rána napříč vesmírem, ale zkrátka změna modelu. V podstatě to dnešní věda ani nijak dál nevysvětluje, a protože matematika funguje, nehledá srozumitelný popis a říká: "Shut up and calculate." Tím ale nechává lidem možnost si donekonečna lámat si hlavu přepálenými představami typu: „Měření“ a „pozorovatel“ mění realitu. A dokonce zdánlivě sugeruje onu strašidelnou dálkovou akci, která se tak nelíbila Einsteinovi. „Částice jsou propojené přes celý vesmír.“ Stačí k tomu neopatrné formulace typu „vlnová funkce se změní naráz všude“ a vzniká dojem nadsvětelného děje, ačkoliv lokální statistiky zůstávají 50/50. To mate i jinak bystré čtenáře. Přitom ta intepretace je postavena jednoduše na tom, že stav je nástroj pro výpočet pravděpodobností; výsledek se rodí až měřením; kolaps je přepis naší předpovědi. Bell porušení tak plyne z neslučitelných měření na sdíleném stavu. Ne akce na dálku, ano okamžitá změna popisu (ryze matematicky, tedy není to fyzikální jev), ale bez fyzikálního účinku nadsvětelnou rychlostí. Tento článek vychází v zásadě ze stejných premis, jako tato převažující kodaňská škola, ale má ambici nabítnout srozumitelnější pohled a jasnější ontologii.

Fyzika bez konce a začátku: Logická spirála k nekonečnu - Blogosvět.cz

www.blogosvet.cz

Co když měl Lorentz pravdu a Einstein se mýlil? Co když éter skutečně existuje, jen ne tak, jak si ho představovali viktoriánští fyzikové? Co když kvantová mechanika není fundamentální popis reality? Hází si starý pán kostkou? Toto není sci-fi, ale legitimní otázky, které si kladou přední fyzikové 21. století. Historie fyziky totiž není příběhem postupného odkrývání pravdy, ale fascinující spirálou, kde se "vyvrácené" ideje vracejí v nových převlecích a kde největší géniové často bojovali nejenom proti svým vědeckým sokům, ale často nakonec i proti důsledkům svých vlastních objevů.

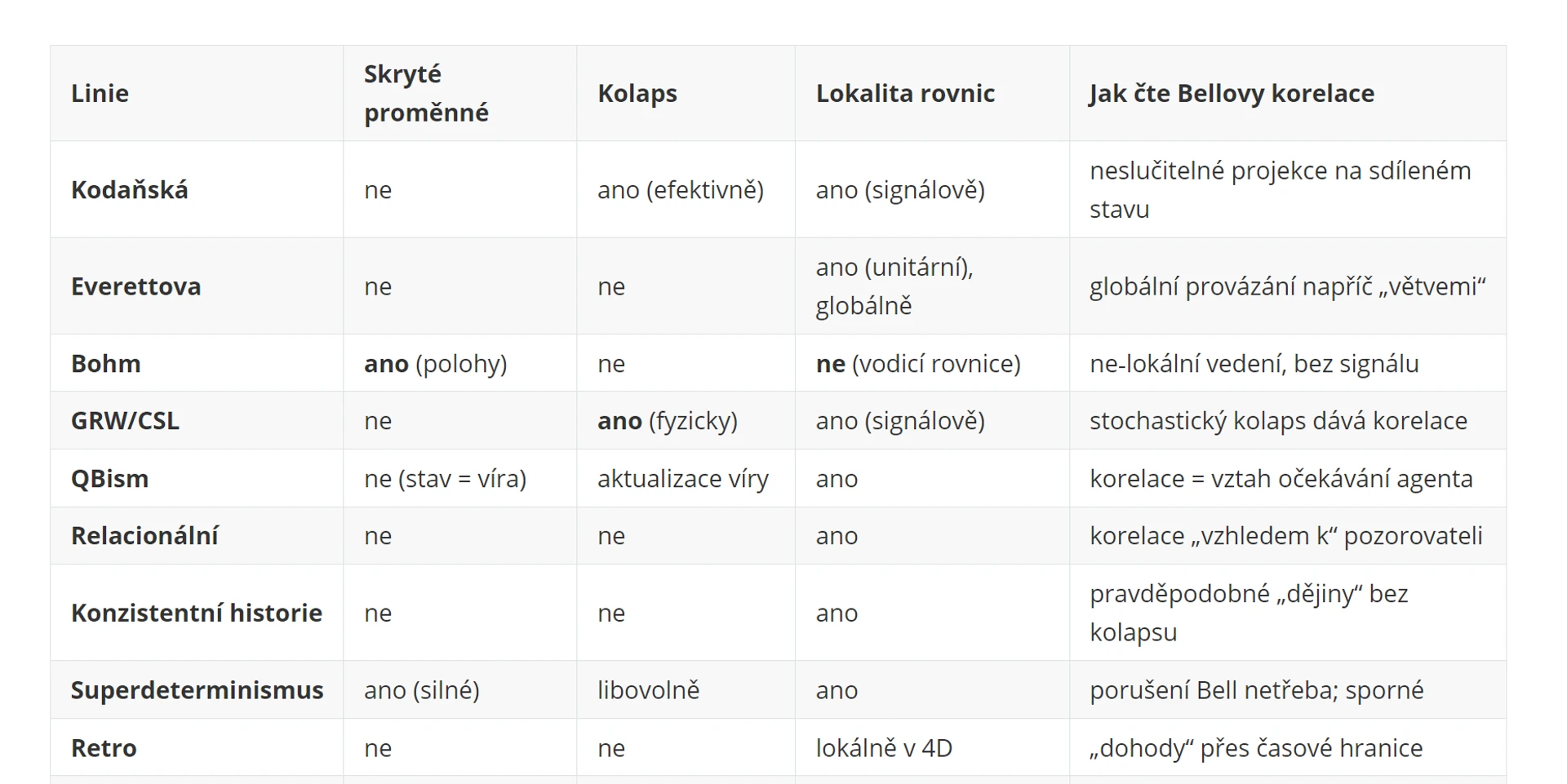
Ale než se k tomu dostaneme, krátce se podívejme i na jiná vysvětlení Bellových nerovností ve kvantových experimentech. Co je al zásadní uvést hned na začátek a co je společné úplně všem teoriím: žádné posílání zpráv nadsvětelně; porušení Bellových nerovností se projeví jen v korelacích, ne v místních statistikách (ty jsou 50/50). Co ale platí je, že každá teorie musí obětovat alespoň jednu ze tří věcí: lokalitu - měření na jedné částici nemůže okamžitě ovlivnit výsledek měření na vzdálené částici, realismus - fyzikální vlastnosti existují nezávisle na měření anebo svobodnou volbu - experimenty lze nastavit nezávisle na skrytých proměnných

Oproti převažující intepretaci, která je v zásadě totožná s tímto článkem (pokud pomineme styl prezenentace), a která porušuje realismus a tvrdí, že hodnoty pro neslučitelná měření vůbec dopředu nemusí existovat, existují i jiné z pohledu intuice "divočejší" přístupy. Ty pak obětují buď lokalitu (tedy propojené děje na více místech současně bez ohledu na rychlost světla) anebo svobodnou vůli (tedy superdeterminismus: samotné měření a jeho výsledky jsou pevně dané dopředu). Z nich možná nejhezčí je ta od Bohm - de Broglie: částice mají přesné polohy a stavy; vlnová funkce je vede deterministicky. Vysvětlení měření bez kolapsu je to, že z evoluce ψ a počátečních poloh dostaneš konkrétní klik detektoru. Cena je ale vysoká: model je nelokální, tedy rychlost částice A závisí okamžitě na nastavení na B (přes společnou ψ v konfiguračním prostoru). Signál sice ani v této interpretaci na dálku "kouzlem" poslat nejde, ale je tam propojení na dálku. To přináší pak jisté komplikaci při reprezentaci světla polem a ne trajektorií a také má jisté obtíže se vyrovnat se speciální teorií relativity. Je ale důležité vědět, že Bellovy nerovnosti lze vysvětlit různými způsoby, ale každý z nich musí něco obětovat z již zmíněné trojice předpokladů, které se intuitivně na první pohled zdají být vytesané do kamene.

Jedna skladba pro dva hlasy

V tomto článku chápeme Bellovy nerovnosti v duchu mainstream pohledu, ale snažíme se je popsat srozumitelně a očistit o "magickou" omáčku. Důležité pro pochopení je, že v kvantové mechanice dvě provázané „částice“ nelze popsat jako dva oddělené objekty s předem dopsanými odpověďmi pro všechna možná měření; chovají se spíš jako dva hlasy jedné společné skladby. Představ si třeba dva kytaristy, kteří secvičili dvojhlas: a teď jeden hraje svůj hlas v Praze, ten druhý v Bratislavě. Každý koncert sám o sobě zní „normálně“ (na každé straně je to obyčejný výsledek 50/50, není to nic neobvyklého). Teprve když je nahraješ a obě nahrávky dáš dohromady, vystoupí původní dvojhlas – u fotonů se pak ten společný vzor neukáže v prostoru, ale v korelacích: a vyjde přesná kosinová křivka podle rozdílu úhlů měření. Dvě samostatné skladby zní najednou jinak. Někdy je celek zkrátka víc než prostý součet jeho částí. V případě Bellovi nerovnosti jde matematicky o to, že amplitudy ze dvou "hlasů" (jsou to ve skutečnosti korelace výsledků měření) se nejprve sečtou a teprve pak se umocní na pravděpodobnost, což vede k jinému a zajímavějšímu výsledku, než by dal jakýkoliv dopředu připravený plán. Žádné kouzlo, žádné dálkové ovládání – jen jiný způsob sčítání: příroda tu nesčítá prosté hotové pravděpodobnosti, ale vlny možností, a to se projeví až v tom, jak spolu ladí výsledky na obou stranách. Zkusme si to tedy popsat a odvodit detailně a jasně.

Bellovy nerovnosti

Bell ukázal, že všechny předem dané plány mají strop: víc shod napříč volbami prostě nedají. Pokusy ale ukazují, že kvantově provázané dvojice na stejné vlně dávají shod víc – přitom bez dálkového ovládání místních výsledků.

Nejde ale nutně o „tajemnou komunikaci na dálku", prosté a srozmitelné vysvětlení je, že se jedná o neklasický vzorec shod. Místní poměry na žádné straně se volbou druhé strany nemění; zvláštnost je až ve společném vyhodnocení párů. A u kvantových vln pak největší rozdíl v souladu oproti předem domluveným odpovědím dostaneš pro čtyři vhodně zvolené směry (např. 0°, 45° proti 22,5° a 67,5°). A tím se dostáváme k jádru pudla: Bellovy nerovnosti jsou prakticky to samé, jako dvojštěrbinové experimenty, které jsou tak krásné a fascinující. Proč? To se dozvíte níže.

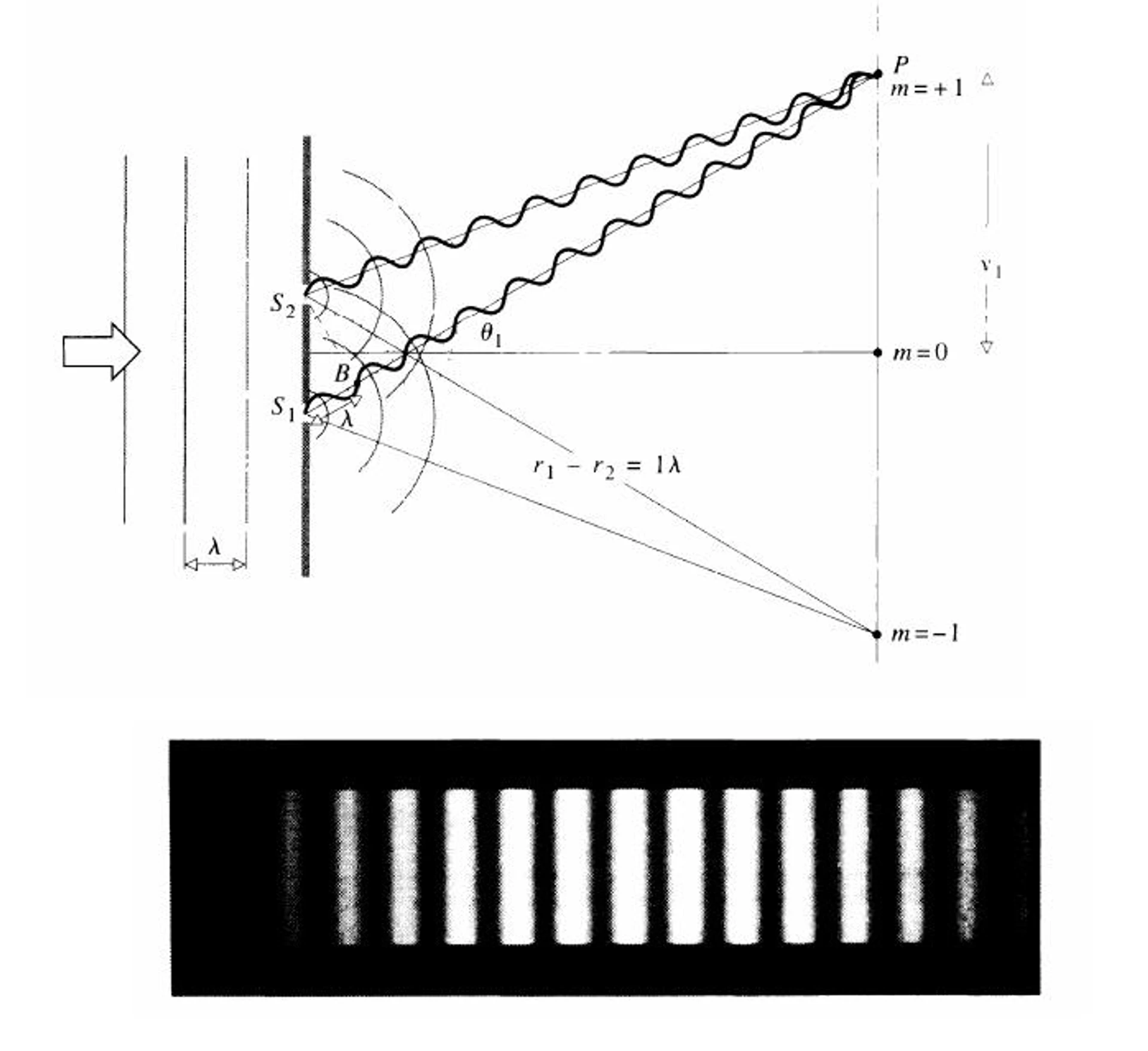
Dvojštěrbina: interference jedné částice

U dvojštěrbiny se amplitudy ze dvou drah sečtou a teprve pak se umocní na pravděpodobnost. Vznikne proužkový obrazec:

?math-inline P(x) \propto \cos^2\phi(x). ?math-inline

Když si vynutíš informaci „kterou štěrbinou šla" (např. detektorem u štěrbiny nebo polarizátory, které značkují dráhu), proužky mizí: sčítají se už jen pravděpodobnosti. Kvantová guma (quantum eraser) umí interferenci obnovit, když informaci o dráze vymažeš – prosté pravidlo: když necháš vlny skládat, obrazec se ukáže.

Kvantová guma: žádná změna minulosti, jen další variace na vlnové téma

Často se tvrdí, že „mění minulost". Nemění. Vezmeme propletený pár. „Signální" foton projde dvojštěrbinou a dráhy označíme polarizací ?math-inline|H\rangle/|V\rangle?math-inline (vodorovná/svislá), tím proužky u jednotlivých detekcí zaniknou. Když ale doprovodný foton změříme v diagonální bázi ?math-inline|\pm\rangle?math-inline (45°), v koincidencích se interference obnoví: podmnožina „signál | doprovodný = ?math-inline+?math-inline " dává proužky ?math-inline\propto \cos^2\phi(x)?math-inline a „signál | doprovodný = ?math-inline-?math-inline " dává komplementární proužky ?math-inline\propto \sin^2\phi(x)?math-inline .

Klíč: Neměníme minulost – signální foton už dopadl. Jen třídíme již naměřená data podle výsledku druhého fotonu. Sečtené dohromady se proužky vyruší, proto každý detektor sám žádné proužky nevidí. Poučení: vzor je v korelacích.

Bell: totéž, ale ve vzoru dvou detektorů

U propletené dvojice fotonů každý detektor sám o sobě dává 50/50, nezávisle na nastavení druhého:

?math-inline P(A=+1\mid a,b)=P(A=+1\mid a)=\tfrac12. ?math-inline

„Proužky" neuvidíš lokálně – objeví se až v koincidencích. Korelace počítáme z četností:?math-inline E(a,b)=\langle AB\rangle=\frac{N_{++}+N_{--}-N_{+-}-N_{-+}}{N_{++}+N_{--}+N_{+-}+N_{-+}}. ?math-inline $

Pro maximálně propletené fotony s lineární polarizací:

?math-inline E(\Delta)=\cos(2\Delta)\quad\text{nebo}\quad E(\Delta)=-\cos(2\Delta),\qquad \Delta=a-b. ?math-inline

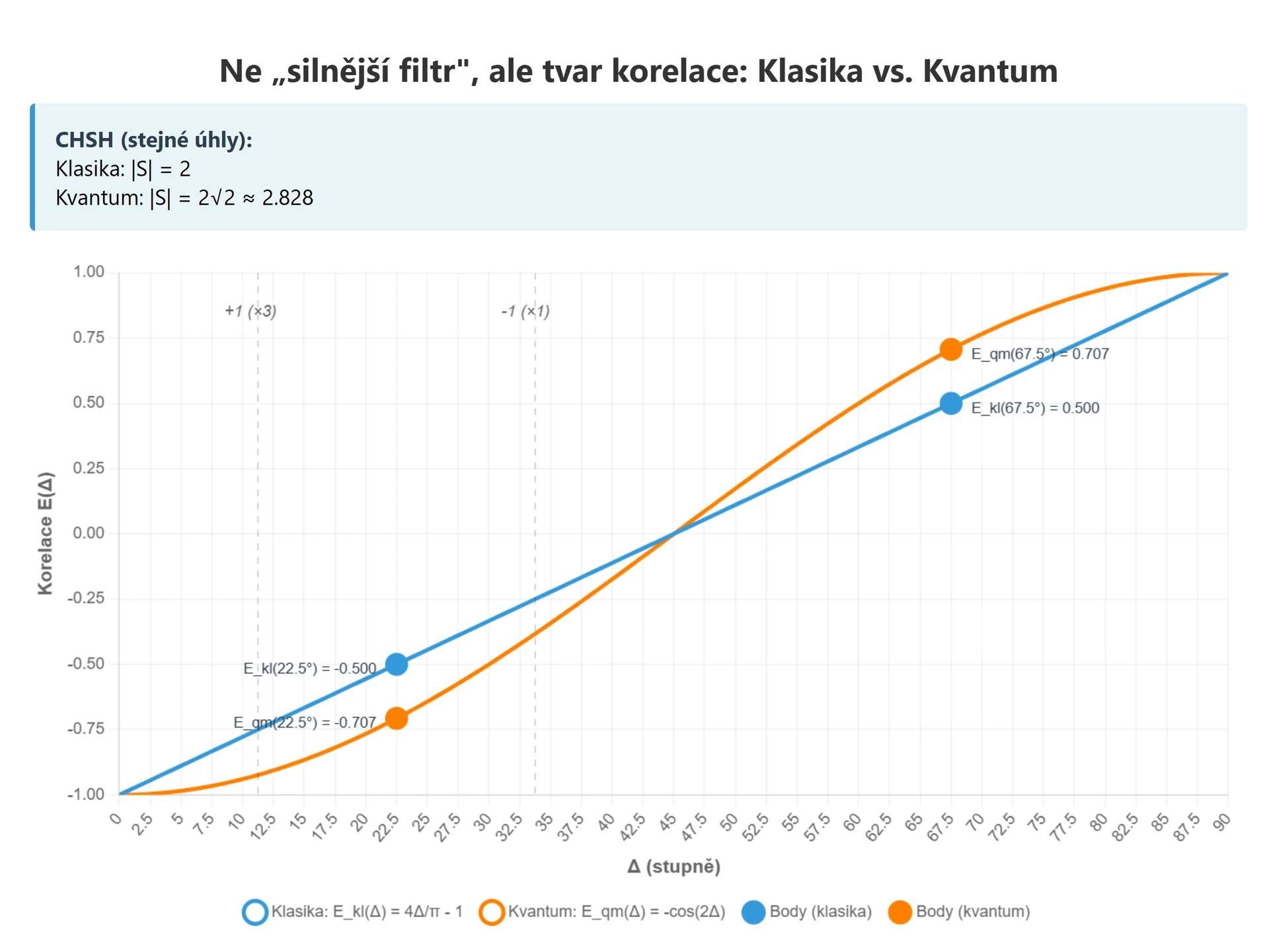
To je „interferenční křivka" ve světě korelací. Kdyby platil lokální „kartičkový" model, vyšel by trojúhelník (po úsecích lineární závislost):

?math-inline E_{\text{LHV}}(\Delta)=1-\frac{4|\Delta|}{\pi}\quad \text{pro } 0\le \Delta\le \frac{\pi}{2},\ \text{perioda } \pi. ?math-inline

Rozdíl tedy není „síla filtru", ale tvar: kosinus vs. trojúhelník.

Proč vyjde ?math-inline2\sqrt{2}?math-inline , a ne jen 2

CHSH kombinace čtyř korelací:

?math-inline S=E(a,b)+E(a,b')+E(a',b)-E(a',b'). ?math-inline

Při volbě ?math-inlinea=0^\circ?math-inline , ?math-inlinea'=45^\circ?math-inline , ?math-inlineb=22{,}5^\circ?math-inline , ?math-inlineb'=-22{,}5^\circ?math-inline platí

?math-inline S=3E(\Delta_1)-E(3\Delta_1),\qquad \Delta_1=22{,}5^\circ=\pi/8. ?math-inline

Lokální plán: pro ?math-inline\Delta_1=\pi/8?math-inline vyjde ?math-inlineS=2?math-inline . Obecně ?math-inline|S|\le 2?math-inline . Kvantum: ?math-inlineS=3\cos(\pi/4)-\cos(3\pi/4)=2\sqrt{2}?math-inline (Tsirelsonova mez). „Kouzlo" je čistě geometrie křivky: zakřivený kosinus umí dát v některých případech (sdílená vlna + neslučitelné projekce + Bornovo pravidlo) větší součet než lineární obálka, která odpovídá našemu přímo pozorovanému makrosvětu.

Co jsou „neslučitelná" měření a proč jsou nutná

Na každé straně volíme dva směry, které nejdou na tomtéž fotonu změřit zároveň. Kdyby šlo všem čtyřem volbám přiřadit jednu společnou tabulku předem daných odpovědí, nutně by platilo ?math-inline|S|\le 2?math-inline . V kvantu taková tabulka neexistuje, a proto může ?math-inlineS?math-inline přesáhnout 2.

Proč to není „strašidelná dálková akce"

Ať nastavíš úhly jakkoli, každý detektor sám vidí přesně očekávaných 50/50 výsledků. Zprávu tím poslat nelze – mění se jen korelace, ne místní statistika. Stejně jako u dvojštěrbinové „gumy": vzor se objeví jen v koincidencích.

Častá mylná interpretace: příklad z časopisu Vesmír

Bohužel se rozšířila mylná interpretace Bellova testu. Dobrým příkladem je článek ve Vesmíru (1998/7) „Kvantové hlavolamy V", který obsahuje hned několik zavádějících tvrzení.

Problém 1: "Foton se dozví a vlnová funkce kolabuje v celém prostoru"

Co je na tom špatně:

"Foton se dozví": Ne, druhý foton se nic "nedozví". Žádná informace mezi fotony neputuje. Místní statistiky druhého fotonu zůstávají přesně stejné (50/50) bez ohledu na to, co naměříte u prvního. * "Vlnová funkce se změní naráz v celém prostoru" - Vlnová funkce není fyzická věc létající prostorem, ale matematický popis našich znalostí o korelacích. Měření prvního fotonu nezmění nic měřitelného u druhého - změní se jen podmíněná předpověď v korelacích; místní poměry zůstávají stejné (50/50). Chybí podstatné: Text nevysvětluje, že druhá strana nepozná, zda už jste měřili. Změna je vidět pouze v korelacích při porovnání záznamů, ne v lokálních měřeních. Proto nelze poslat zprávu.

Správnější vysvětlení: Měřením jednoho fotonu získáme pouze jeden výsledek (+1 nebo -1). Druhý foton se chová úplně stejně jako předtím - jeho lokální statistiky zůstávají 50/50. Teprve když změříme oba fotony a porovnáme výsledky, objeví se interference v korelacích - ukáže se v nich vlnový průběh (kosinus), ne klasicky očekávaná lineární závislost. Žádný foton se nic "nedozví", vlnová povaha se projeví až při společném vyhodnocení.

Problém 2: Analogie s televizí a porodností

Proč je to zavádějící:

Není to vůbec Bellův test: Bellův test je pár po páru, s náhodnou volbou pro každý pár. Tady je jedna volba na den a součty mnoha nesouvisejících událostí. Chybí párování Praha–Olomouc po jednotlivých pokusech. Nesprávný závěr: tvrzení, že „pravděpodobnost v Praze závisí na programu v Olomouci", by znamenalo možnost posílat zprávy přepínáním programu. To je špatně. V Belle platí: místní poměry se nemění, mění se jen společný vzor shod/neshod v párových datech. Poznámka pod čarou to sice mírní, ale v hlavním textu vzniká dojem „dálkového ovládání". Ten je chybný.

Mikroskopický pohled: „dvojštěrbina rozdělená mezi dva detektory"

Pro stav ?math-inline|\Phi^+\rangle=\tfrac{1}{\sqrt{2}}(|HH\rangle+|VV\rangle)?math-inline je amplituda výsledku „++" při měření v úhlech ?math-inlinea,b?math-inline :

?math-inlineA_{++}=\frac{1}{\sqrt{2}}(\cos a\cos b+\sin a\sin b)=\frac{1}{\sqrt{2}}\cos(a-b).?math-inline

Pravděpodobnost je ?math-inline\tfrac12\cos^2(a-b)?math-inline . Analogicky pro „--". Součet dvou „cest" (HH a VV) interferuje a dává ?math-inline\cos(2\Delta)?math-inline v korelaci ?math-inlineE?math-inline . Interference se neukáže v prostoru, ale ve vzoru korelací.

Širší kontext

Existují hypotetické korelace bez možnosti posílat zprávy, které by v CHSH daly až ?math-inlineS=4?math-inline (Popescu–Rohrlichova krabička, PR‑box). CHSH je Clauser–Horne–Shimony–Holt formalizace Bellova testu, která je formálně ještě dokonalejší.) Každý výstup by byl sám 50/50 (ani zde zpráva nejde přímo poslat), ale korelace by byly ještě silnější než kvantové. Příroda takové korelace ale nedovoluje – drží se Tsirelsonovy meze ?math-inline2\sqrt{2}?math-inline antová pravidla samotná jsou zcela v souladu s očekávatelnými přírodními zákony, i když mohou být trochu matoucí: bez zpráv, ale ani ne „maximálně" nelokální.

Proč to není paradox, ale maximum možného

Bellovy korelace nejsou paradox, ale maximum, které ještě respektuje nemožnost přenosu „informace zdarma": informační kauzalita říká: když Alice pošle Bobovi ?math-inlinem?math-inline klasických bitů, Bob z toho nemůže získat víc než ?math-inlinem?math-inline bitů náhodně přístupné informace – i kdyby sdíleli libovolné předem domluvené zdroje. Kvantová mechanika tento princip dodržuje, a má totožnou ostrou mez ?math-inlineS\le 2\sqrt{2}?math-inline . Hypotetické „superkvantové" korelace (PR‑box) by ji porušily a byly by rozporu s přírodními zákony, které jsme zatím poznali. Příroda tak vysoko ale nejde a o žádné strašidelné porušení přírodních zákonů v případě Bellova testu nejde.

Nejnovější pokusy

Bell bez provázání?

Nedávný nový experiment (Science Advances, 2025) ukazuje na možné porušení Bellovy nerovnosti s neprovázanými páry tak, že více zdrojů světla a optika po cestě vytvoří "nerozlišitelnost drah". Interference se ani tady neprojeví lokálně (vše stále 50/50), ale jen ve čtyřnásobných koincidencích – opět jako u dvojštěrbiny: tedy když necháš vlny možností skládat, ukáže se v korelacích pravděpobnosti vzor. Interference v korelacích tu není trik filtrů, ale překryt dvou různých možností vzniku vlny, které nelze odlišit: „pár vznikl v (I,II)“ nebo „v (III,IV)“ a v tomto případě je vzhledem ke zvoléné metodě viditelnost kosinové korelace nižší než u klasického Bell testu, jako ho provedl třeba Aspect, tedy jen zhruba 80%. I tak vede k S > 2. Pozor ale na použitou metodiku v jejich experimentu: „mínus 1“ se bere z doplňkového nastavení a s dodatečným výběrem dat, což je v CHSH nestandardní a je předmětem odborné kritiky (možný výběrový klam). Směr je to ale zajímavý, jen skutečně „bezcedníkové“ ověření tomu zatím chybí. Každopádně i pro tento pokus platí nosná teze tohoto článku: „interference vlnových funkcí se neprojeví u Bellovy testu v prostoru, ale ve vzoru korelací.“ Experiment Wangova týmu je zajímavý v tom že rovnou navrhuje způsob, jak interference vyroste i bez párového provázání – a sice díky totožnosti drah u čtyř fotonů.

MIT experiment: Einstein se mýlil… staletá debata rozhodnuta

Možná jste nedávno zaznamenali články, které se dostaly do mnoha médií a zněly bombasticky. Skutečnost ale je podstatně méně zajímavá: , ale učebnicově čistý důkaz staré poučky: víc víme „kterou‑cestou“ ⇒ méně interferenčních proužků. Elegantní a skvělá laboratorní práce, ale oprvadu žádná revoluce.

Co tedy MIT dokázali:

Povedla se jim zatím nejčistší verze dvojštěrbiny: „štěrbiny“ jsou dva jednotlivé atomy, světlo je tak slabé, že každý atom rozptýlí nanejvýš jeden foton. Měřili, jak informace o dráze snižuje kontrast interferenčních proužků. Potvrdili komplementaritu (víc dráhy → míň interference). Je to jednočásticová interferometrie, ne test skrytých proměnných na dálku. Je to skvělý, čistý pokus s dvěma atomy coby „štěrbinami“ hezky potvrzuje komplementaritu: čím víc víš o dráze, tím menší jsou proužky. Ale není to žádné „uzavření stoletého sporu“ ani „Einstein byl vedle“ — EPR/Bell se tu neřeší a Einstein sám počítal s rekoilem štěrbiny. Je to elegantní zpřesnění známého: interferenci zabíjí informace o cestě, ne skrytá dálková akce. Dva jednotlivé atomy hrají roli dvou štěrbin. Posíláme na ně velmi slabé světlo, aby každý atom rozptýlil nanejvýš jeden foton. Když o „které dráze“ fotonu atom nic neví (je dobře lokalizovaný), interference na kameře má vysoký kontrast – jasné proužky. Když atom může nést informaci o dráze (větší „rozmazání“ v pasti), kontrast klesá: víc znalosti o cestě ⇒ méně interferenčního vzoru. To je přímé potvrzení komplementarity: informace o dráze a interferenční obrazec se vylučují. Není v tom žádné dálkové působení – jde o místní kvantovou korelaci foton–atom, která buď zachová, nebo zničí koherenci. Pointa je stejná jako v celém článku: příroda skládá vlnové příspěvky; když dovolíme „čtení dráhy“, skládání se rozladí a proužky mizí.

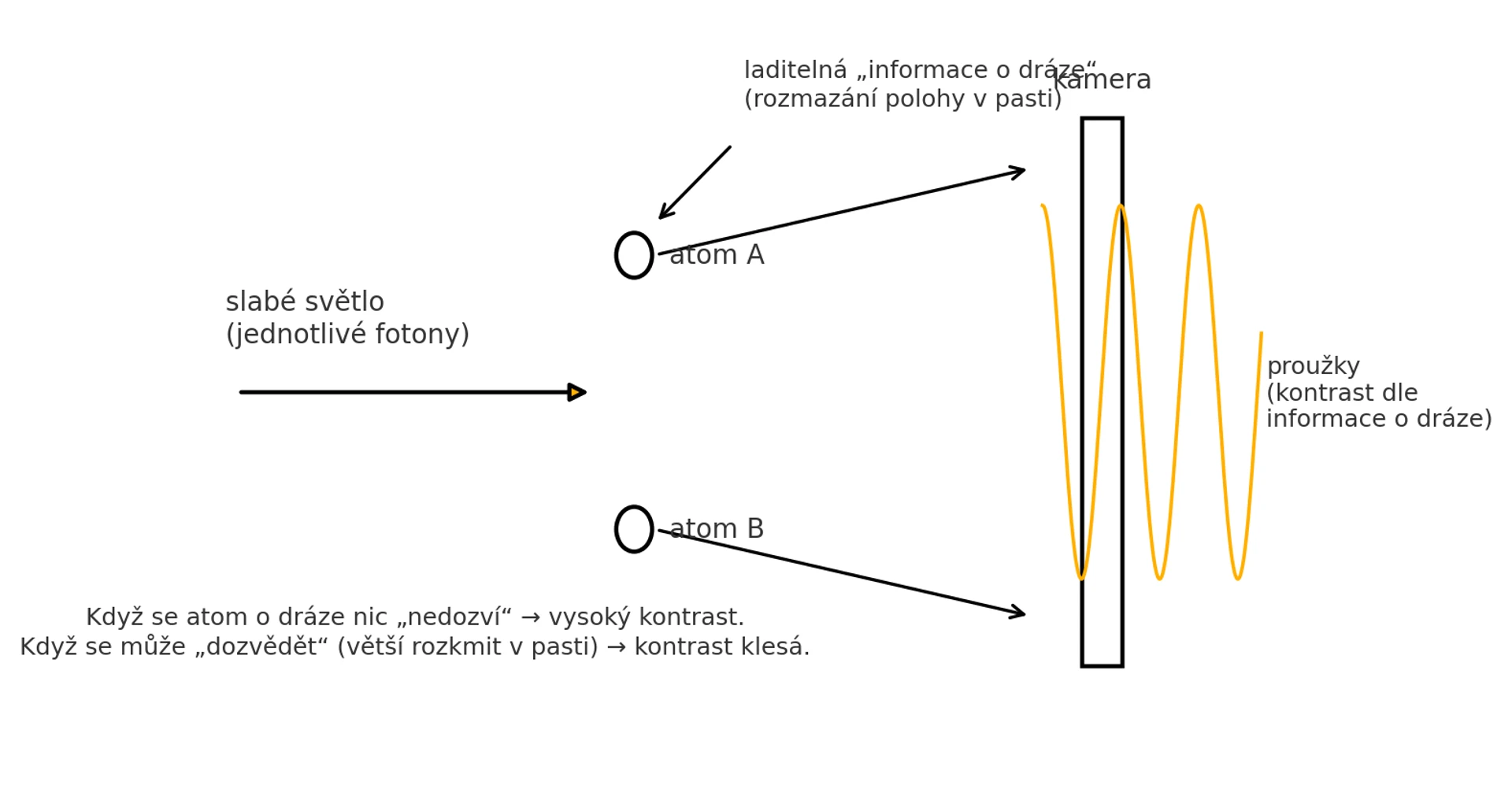
Co z toho neplyne:

Neuzavírá to „stoletý spor“ v tom smyslu EPR/Bell a tvrzení „Einstein byl vedle“ je hloupá zkratka. Einstein sám přišel s myšlenkou rekoilující štěrbiny (získáš‑li informaci o dráze, interferenci ztratíš) a přesně tohle čistě ověřuje i tento experiment. Sporné bylo jak a proč se to děje, ne zda dvojštěrbina dává proužky. MIT „jen“ potvrzuje Bohrův princip komplementarity v ideálních podmínkách. Titulky typu „MIT vyřešil 100letý spor / Einstein se mýlil“ jsou bombastické clickbait PR. Vlastní MIT papír říká přesně, že šlo o „nejvíc idealizovanou“ verzi pokusu, která potvrzuje standardní kvantový obrázek.

Proč jsou bombastické titulky mimo

„Einstein was wrong… settled a 100‑year debate“ je mediální přepal; článek MIT mluví čistě o „holds up when stripped to its quantum essentials“ – tedy že dvojštěrbina obstojí i v nejčistší verzi. Ne „zvrat“, ale vyčištění experimentu. „Light has two identities that are impossible to see at once“ je v jádru jen přebalená komplementarita (známá desítky let); novinka je technická čistota provedení, ne nový zákon.

Tahák: Co si zapamatovat z tohoto článku

Klíč Bellova testu je sdílená vlna + neslučitelné projekce + Bornovo pravidlo. Z toho nutně vyleze kosinusová korelace E(Δ), lokálně ale výsledky nemění a jsoupořád 50/50, a v CHSH je maximum: ?math-inline|S|\le 2\sqrt{2}\approx 2{,}83?math-inline , bez jakékoliv strašidelné akce na dálku.

Hlavní myšlenka je tato: Bellův test je ve své podstatě stejný fyzikální jev, jako „dvojštěrbina pro dva": příroda skládá vlny možností, ne jen pravděpodobnosti. Propletení a neslučitelná měření dávají kosinusový tvar korelace, který u vybraných úhlů sčítá na ?math-inline2\sqrt{2}?math-inline , zatímco každý klasický „kartičkový" plán se zastaví na 2. Stejně jako u dvojštěrbiny s „gumou": když dovolíš vlnám koherentně se skládat, obrazec vyskočí – tady ne na stínítku, ale v číslech ?math-inlineE(\Delta)?math-inline .

• Klasický limit: ?math-inline|S|\le 2?math-inline

• Kvantový limit: ?math-inline|S|\le 2\sqrt{2}\approx 2{,}83?math-inline

• Informační limit: ?math-inline|S|\le 2\sqrt{2}?math-inline

• Každý detektor sám: vždy 50/50, samotné měřitelné výsledky jsou shodné pro klasické jevy i pro ty kvantové

Podstata: Interference se neprojeví v prostoru, ale ve vzoru korelací. Žádná komunikace, žádná magie – jen dvě různé částice, které jsou na stejné vlně. Nejde o dvě oddělené vlny, ale o jednu společnou „vlnu" pro celou dvojici; právě tohle vlnové souznění dělá ten nezvykle silný soulad. Místně se nic nemění a žádné zprávy na dálku nadsvětelnou rychlostí tím opravdu posílat nejdou. Ani to nesouvisí s naším vědomím či vnímáním.